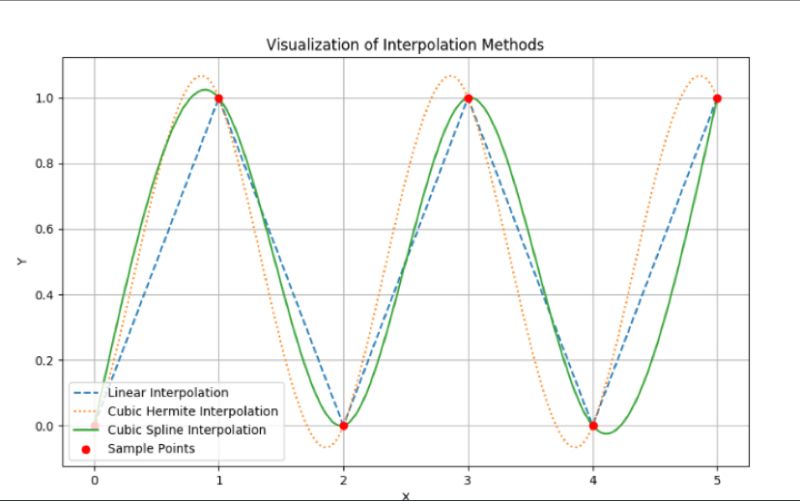
Linear Interpolation:
Imagine you're drawing a straight line between two points on a graph. If you want to find out the value of a point that lies between these two points, you just see where it lands on that straight line. That's linear interpolation. It's like connecting dots on a graph with straight lines.
Cubic (Bessel) Hermite Interpolation:
Let's say you're not only interested in passing through some points on a graph, but you also care about the angle (or slope) at which you hit those points. This method ensures that not only does the curve pass through the given points, but it also takes into account a specific direction or slope at those points. Imagine it as trying to drive a car through checkpoints at specific angles instead of just passing through them.
Cubic Spline Interpolation:
Imagine you have multiple dots on a piece of paper, and instead of drawing straight lines between them, you use a flexible, bendy ruler that tries to smoothly connect all these dots. The ruler adjusts its curvature to ensure the smoothest and most natural connection between all points. That's cubic spline interpolation. The curve might not be as "tight" to each point as with Hermite, but it ensures a smoother overall journey.
- Linear: Connects points with straight lines.
- Cubic Hermite: Connects points with curves, paying attention to specific angles at those points.
- Cubic Spline: Connects points with smooth curves, ensuring a gentle and seamless overall journey.
Interpolation techniques, are widely utilized in the domain of financial engineering, especially in option pricing:
Volatility Smile & Surface: When options are priced, implied volatilities often don't remain constant across different strike prices and maturities. Interpolation techniques are used to estimate implied volatilities for strike prices or maturities that might not be directly quoted in the market.
Yield Curves: When discounting future cash flows, especially for options on interest rates, we often rely on a yield curve. However, the yield curve is typically constructed from a set of discrete market data points. To get a smooth continuous curve, or to estimate rates for maturities not in the dataset, interpolation is used.
Numerical Methods:
Many option pricing methods, especially those used for exotic options, rely on numerical methods like finite difference or binomial trees. When moving between nodes, interpolation can help estimate values between discrete points.
Calibration: Advanced option pricing models often require calibration to market data. This calibration can involve volatility surfaces where interpolation assists in filling gaps between observed market data points.
Replicating Portfolios: In creating a replicating portfolio for an option, one might need to value bonds or other instruments that don't match standard market maturities or strike prices. Interpolation can assist in these valuations.

Écrire commentaire