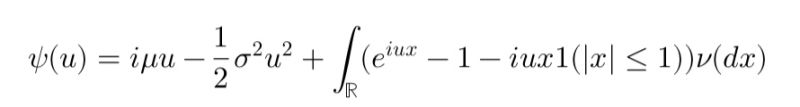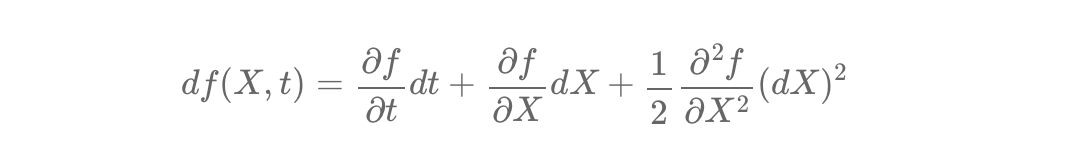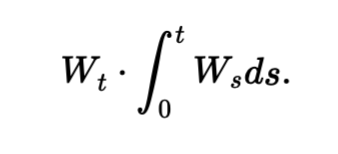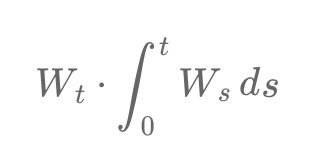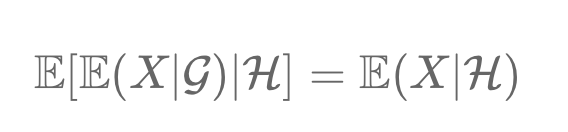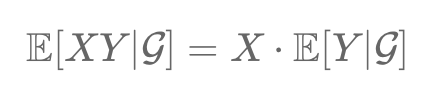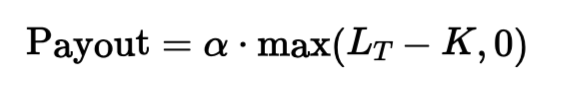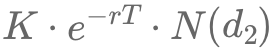Stochastic Models and Processes
Stochastic Models and Processes · 07. January 2025
Taylor Expansion and Itô's Lemma are fundamental tools for modeling deterministic and stochastic systems. Taylor Expansion provides approximations for smooth and predictable systems, while Itô's Lemma adapts these principles to account for randomness, a critical feature in financial modeling.
Stochastic Models and Processes · 17. June 2024
Comprenez l'interaction complexe entre le processus de Wiener \( W_t \) et son intégrale ∫ de 0 à t \( W_s \) ds. Ce produit stochastique nécessite des outils comme le lemme d'Itô pour analyser sa nature non linéaire. La covariation quadratique éclaire le comportement conjoint de ces processus, essentiel pour le pricing d'options exotiques, comme les options asiatiques.
Stochastic Models and Processes · 10. June 2024
La formule de Black-Scholes pour une option d'achat calcule le prix de l'option en utilisant la probabilité d'exercer l'option, représentée par N(d2). Cette probabilité ajustée au risque assure une tarification sans arbitrage. Un N(d2) plus élevé signifie une probabilité accrue d'exercice de l'option, affectant le coût attendu et la valeur nette de l'option.
Stochastic Models and Processes · 19. November 2023
Multiplying a Wiener process W_t by its integral creates a complex stochastic process, combining an instantaneous, "memoryless" state with its cumulative history. This nonlinear product, needing tools like Itô's lemma for analysis, reveals interactions between the current state and past values, crucial in financial mathematics for pricing path-dependent options.
Stochastic Models and Processes · 19. November 2023
The Tower Property in probability theory simplifies conditional expectations. It states that refining information from a broader σ-algebra (𝒢) to a narrower one (H) yields the same expectation as directly using H. In finance, it means mid-year portfolio predictions remain valid regardless of additional end-year information. This principle aids in effective portfolio management and risk assessment.
Stochastic Models and Processes · 19. November 2023
Conditional expectation, 𝔼(X|𝒢), in probability theory, is defined within a probability space (Ω, F, P). It's the expected value of a random variable X given a sub-σ-algebra 𝒢 of F, offering insights based on additional information. This concept is vital in analyzing stochastic processes, aligning with the structure and constraints of 𝒢.
Stochastic Models and Processes · 14. November 2023
A caplet is a financial derivative, akin to a call option, used for hedging against interest rate increases. It pays out if the interest rate exceeds a predetermined rate (K) at the end of a period. The payout, calculated as α * max(LT - K, 0), depends on the period's interest rate (LT) and the day count fraction (α), reflecting the time span of the caplet. It effectively caps the borrower's interest rate costs, ensuring they don't exceed the strike rate K
Stochastic Models and Processes · 14. November 2023
In the Black-Scholes model, N(d2) calculates the probability of a call option being in the money at expiration, balancing its potential profitability and expected exercising cost. This risk-neutral measure assumes investments grow at a risk-free rate, crucial for arbitrage-free option pricing. #BlackScholesModel #RiskNeutralValuation #OptionPricing #N(d2)Explained
Stochastic Models and Processes · 14. November 2023
In risk-neutral valuation, predicting the next step in a random walk, even with real probabilities of 0.55 up and 0.45 down, is not straightforward. The expected direction—up, down, or indeterminate—depends on additional factors like the risk-free rate and the magnitude of movements.
Stochastic Models and Processes · 13. November 2023
In the Black-Scholes formula, Δ is the option delta, showing the price change of a call option for a $1 change in the stock price. Δ equals N(d1), where N is the cumulative normal distribution function, and d1 factors in the stock price, strike price, time to expiration, risk-free rate, and volatility.
#OptionsTrading #Delta #BlackScholesModel