Understanding Subadditivity
Subadditivity is a principle in risk management that suggests combining two or more risky assets should not result in a total risk greater than the sum of the individual risks. This concept arises from the idea that diversification typically reduces risk.
Mathematically, subadditivity can be expressed as:
\[ \rho(A + B) \leq \rho(A) + \rho(B) \]
Here:
- \( \rho \): Represents the risk measure.
- \( A \) and \( B \): Represent different assets or portfolios.
If the total risk (\( \rho \)) of the combined portfolio (\( A + B \)) is less than or equal to the sum of the risks of the individual portfolios (\( A \) and \( B \)), the risk measure is considered subadditive.
Subadditivity in Coherent Risk Measures
Subadditivity is one of the key properties that a risk measure must have to be considered a coherent risk measure. However, not all popular risk measures satisfy this property.
Value at Risk (VaR), for example, is often criticized for not always meeting the subadditivity condition. VaR is calculated as a specific percentile of the loss distribution — for instance, the 95th percentile. It measures the loss that is not exceeded with a certain confidence level (e.g., 95% of the time).
However, VaR fails to provide information about the potential size or frequency of losses that exceed this level, often referred to as "tail risk"1.
Example: Lack of Subadditivity in VaR
Consider two bonds, each with:
- Default probability: 4%.
- Notional value: $10 million.
- Loss given default: 100%.
At a 95% confidence level, the VaR for each bond individually is zero because the default probability (4%) is less than the threshold (5%). However, to determine the VaR for the combined portfolio, we calculate the probability of at least one bond defaulting.
The probability that neither bond defaults is:
\[ (1 - 0.04) \times (1 - 0.04) = 0.9216 \]
Therefore, the probability of at least one bond defaulting is:
\[ 1 - 0.9216 = 0.0784 \, \text{or} \, 7.84\%. \]
Since this probability (7.84%) exceeds the 5% threshold, the combined VaR equals the full notional value of $10 million. This example illustrates that VaR is not subadditive and fails to reflect the diversification benefit.
CVaR: A Subadditive Alternative
Conditional Value at Risk (CVaR) addresses the shortcomings of VaR by measuring the average expected loss in the worst-case scenarios beyond the VaR threshold. CVaR accounts for the "shape" and severity of the tail risk, providing a more comprehensive risk assessment.
Unlike VaR, CVaR is subadditive, making it a preferred choice in risk management when diversification benefits need to be accurately reflected.
While VaR remains a widely used risk measure, its failure to satisfy subadditivity highlights its limitations in capturing diversification effects. In contrast, CVaR provides a robust alternative, addressing both the magnitude and distribution of extreme losses while respecting the subadditivity property.
1 Tail risk: Refers to the risk of extreme outcomes or losses in the tails of a probability distribution, beyond the typical confidence intervals.
🎓 Formation recommandée : Les fondamentaux de la Finance Quantitative
Découvrez les concepts essentiels de la finance quantitative, explorez les modèles mathématiques appliqués et apprenez à les utiliser pour la gestion des risques et la valorisation des actifs.
Découvrir la formation

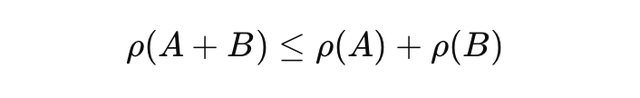
Écrire commentaire