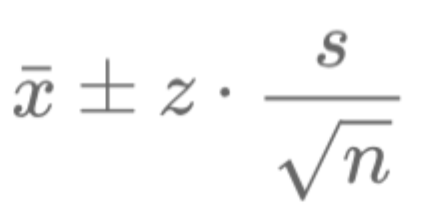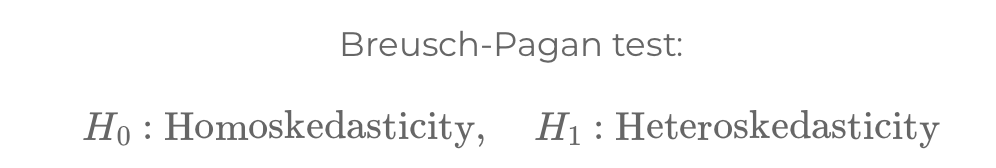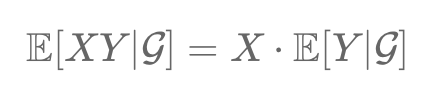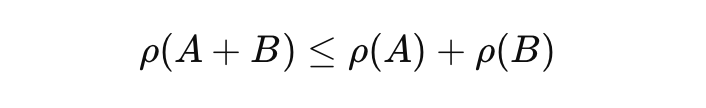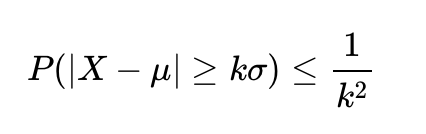Statistics · 10. décembre 2024
Gaussian copulas fail to capture extreme co-movements, a limitation revealed during the 2008 crisis. While Pearson correlation measures average linear relationships, it overlooks tail dependencies. Tail dependence coefficients (\( \lambda_U \), \( \lambda_L \)) quantify the probability of simultaneous extremes, critical in financial stress. Senior CDO tranches, seen as low-risk under Gaussian models, suffered heavy losses due to hidden tail risks with junior tranches.
Statistics · 07. décembre 2024
Confidence intervals are essential tools in finance, helping quantify uncertainty in statistical estimates like mean returns, interest rates, or volatility. They provide a range where the true population parameter is likely to fall, aiding in decision-making and performance comparisons. This article explains confidence intervals in simple terms, covering their definition, calculation, and role in finance.
Statistics · 14. février 2024
In regression analysis, heteroskedasticity and autocorrelation significantly impact model accuracy. Heteroskedasticity involves variable error variances, while autocorrelation means time-correlated residuals, both requiring tests like Breusch-Pagan and Durbin-Watson for detection and correction.
Stochastic Models and Processes · 19. novembre 2023
Conditional expectation, 𝔼(X|𝒢), in probability theory, is defined within a probability space (Ω, F, P). It's the expected value of a random variable X given a sub-σ-algebra 𝒢 of F, offering insights based on additional information. This concept is vital in analyzing stochastic processes, aligning with the structure and constraints of 𝒢.
Mathematical Principles and Quantitative Finance · 14. novembre 2023
The Subadditivity Principle in risk management states that combined asset risks shouldn't surpass individual risks, highlighting diversification's role in reducing risk. This principle contrasts with Value at Risk (VaR), which often overlooks 'tail risks', making it non-subadditive. Conditional VaR (CVaR) addresses this by considering severe losses beyond VaR, ensuring a more accurate risk measure.
Statistics · 11. novembre 2023
Chebyshev's inequality, vital in probability theory and finance, estimates the probability of a variable deviating from its mean by more than k standard deviations, capped at 1/k². Useful in finance for risk analysis and asset allocation, it applies to various distributions without needing a normal distribution assumption. However, it may overestimate extreme outcomes, leading to conservative strategies. #ChebyshevsInequality #QuantitativeFinance #RiskManagement #FinancialAnalysis
Stochastic Models and Processes · 02. octobre 2023
Gaussian Process Regression demystified: a statistical tool predicting outcomes by learning patterns from data. Imagine a wise elder foreseeing future events based on past experiences, ensuring precision. Ideal for forecasting trends! #DataScience #Statistics #Prediction
17. septembre 2023
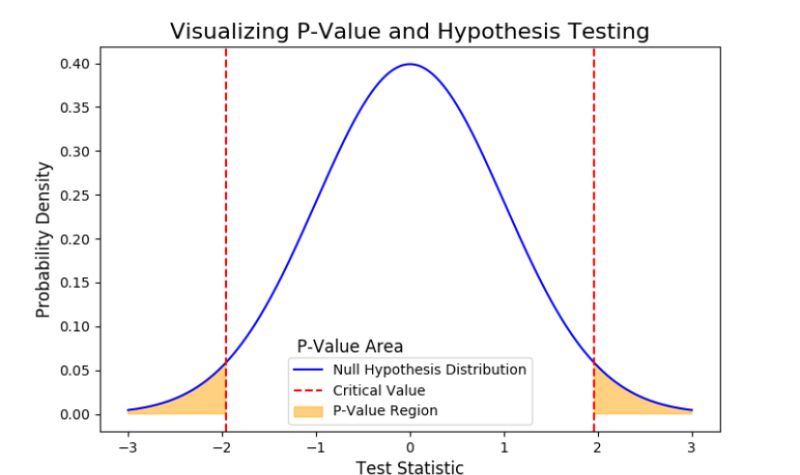
Unlock the mystery of copula in pairs trading and the p-value in hypothesis testing with our concise guide. Learn how copula aids in understanding dependencies and the p-value’s role in evaluating evidence against the null hypothesis, all explained simply. Stay informed and empowered in your trading and data analysis. #Copula #PValue #PairsTrading #DataAnalysis