Le modèle de Black-Scholes est l’un des cadres les plus influents pour la valorisation des options européennes. Au cœur de ce modèle, deux probabilités jouent un rôle fondamental : \( N(d_1) \) et \( N(d_2) \). Bien qu'elles soient toutes deux définies comme des fonctions de répartition cumulées de la loi normale standard, elles remplissent des rôles distincts dans l’évaluation des options d’achat et de vente.
Alors que \( N(d_2) \) représente la probabilité, sous la mesure risque-neutre, que l’option expire dans la monnaie (in the money), \( N(d_1) \) ajuste cette probabilité en tenant compte de l'espérance conditionnelle du prix du sous-jacent si l’option est exercée. Comprendre ces deux notions est essentiel pour saisir la mécanique de la formule de Black-Scholes et l’interaction entre valeur intrinsèque et valeur temps dans le pricing des options.
Cet article explore les différences entre \( N(d_1) \) et \( N(d_2) \), leur contribution à la valorisation des options, et pourquoi l’inégalité \( N(d_1) > N(d_2) \) garantit une tarification sans arbitrage.
Composants clés de la formule de Black-Scholes
La formule de Black-Scholes pour une option d'achat européenne est donnée par :
\[ C = S \cdot N(d_1) - X \cdot e^{-rT} \cdot N(d_2) \]
où :
- \( C \) : Prix de l'option d'achat
- \( S \) : Prix actuel du sous-jacent
- \( X \) : Prix d'exercice
- \( r \) : Taux d'intérêt sans risque
- \( T \) : Temps restant jusqu'à l'échéance
- \( N(d_1) \), \( N(d_2) \) : Fonctions de répartition cumulées de la loi normale standard
Les probabilités \( N(d_1) \) et \( N(d_2) \) sont essentielles pour déterminer la valeur de l'option :
- \( N(d_2) \) : Probabilité, sous la mesure risque-neutre, que l'option expire dans la monnaie (\( S_T > X \)).
- \( N(d_1) \) : Mesure ajustée du risque, prenant en compte l'espérance conditionnelle du prix du sous-jacent en cas d'exercice.
Intuition derrière \( N(d_1) \) et \( N(d_2) \)
Pour bien comprendre les rôles de \( N(d_1) \) et \( N(d_2) \), examinons les deux principaux termes de la formule de Black-Scholes :
- \( S \cdot N(d_1) \) : Représente la valeur actuelle du sous-jacent, ajustée pour tenir compte de la probabilité d'exercice. \( N(d_1) \) intègre à la fois la probabilité d'exercice et l'espérance conditionnelle du prix du sous-jacent lorsque l'option est dans la monnaie.
-
\( X \cdot e^{-rT} \cdot N(d_2) \) : Correspond à la valeur actualisée du prix d'exercice, pondérée par la probabilité que l’option soit exercée (\( N(d_2) \)).
La différence entre ces deux termes détermine la valeur de l'option. L'inégalité \( N(d_1) > N(d_2) \) garantit que \( S \cdot N(d_1) \) est toujours supérieur à \( X \cdot e^{-rT} \cdot N(d_2) \), assurant ainsi une valeur non négative pour l’option.
Pourquoi la relation \( N(d_1) > N(d_2) \) est-elle essentielle ?
L’inégalité \( N(d_1) > N(d_2) \) reflète le fait que \( N(d_1) \) prend en compte l'espérance conditionnelle du prix du sous-jacent, tandis que \( N(d_2) \) ne considère que la probabilité d'expiration dans la monnaie. Cette correction assure que la valeur de l’option ne repose pas uniquement sur la probabilité d'exercice, mais aussi sur le gain potentiel qu'elle peut générer.
La distinction entre \( N(d_1) \) et \( N(d_2) \) met en lumière l'équilibre entre la valeur intrinsèque (déterminée par l’écart entre le prix du sous-jacent et le prix d'exercice) et la valeur temps (le potentiel de l'option à gagner en valeur avant l’échéance).
Le modèle de Black-Scholes constitue un cadre robuste et largement utilisé pour la valorisation des options européennes. Son succès repose en grande partie sur les rôles précis de \( N(d_1) \) et \( N(d_2) \), qui permettent une tarification cohérente sous la mesure risque-neutre. En comprenant ces notions, les investisseurs et analystes peuvent mieux interpréter la valeur des options et élaborer des stratégies de couverture efficaces.
🎓 Recommended Training: The Fundamentals of Quantitative Finance
Discover the essential concepts of quantitative finance, explore applied mathematical models, and learn how to use them for risk management and asset valuation.
Explore the Training
🎓 Recommended Training: The Fundamentals of Options
Discover the role and mechanics of options, how to use them, and learn to interpret the Greeks.
Explore the Training

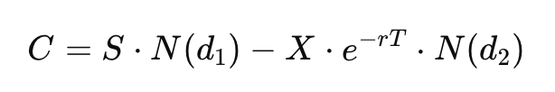
Écrire commentaire