Stochastic Models and Processes · 10. novembre 2023
Convertible bonds blend debt and equity, featuring an option to convert into a set number of shares. Key factors include conversion ratio and price. Valuation hinges on stock dynamics, credit risk, and hazard rate. At maturity, value is the higher of face value or conversion outcome. Monte Carlo simulations help in pricing, considering callability and putability options. #ConvertibleBonds #CreditRisk #FinancialModeling #InvestmentStrategies
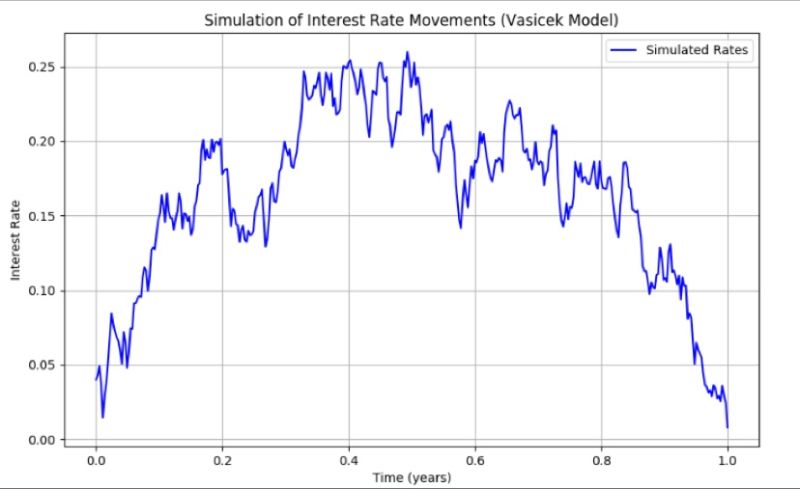
Stochastic Models and Processes · 01. novembre 2023
The Vasicek model predicts interest rates using mean reversion, volatility, and the speed of reversion. Its equation, dr(t) = κ(θ - r(t)) dt + σ dW(t)`, models rates' return to a mean (θ) with volatility (σ) and randomness (dW(t)). It's vital for financial strategies and simulations.