Sklar's Theorem, introduced in 1959, revolutionized multivariate analysis by enabling the separate modeling of individual distributions and their interdependencies, reshaping probabilistic modeling and risk management. Consider a set of random variables, \( X_1, X_2, \dots, X_N \). Each variable has its own behavior, modeled by a distribution function, denoted as \( F_{X_i}(x) \) for the \( i \)-th variable. These functions, known as marginal distributions1, describe the probability that \( X_i \) will take a value less than or equal to \( x \) independently of other variables.
A copula2 is a mathematical function that links univariate marginals to form their multivariate distribution. The beauty of copulas lies in their ability to model the dependency structure of variables separately from their margins.
Sklar's Theorem states that for any multivariate cumulative distribution function \( F \) with given marginals, there exists a copula \( C \) such that for any vector \( (x_1, x_2, \dots, x_N) \), the joint distribution can be written as:
\[ F(x_1, x_2, \dots, x_N) = C(F_{X_1}(x_1), F_{X_2}(x_2), \dots, F_{X_N}(x_N)) \]
We then say that \( F \) has \( C \) as its copula.
What makes Sklar's Theorem particularly powerful is the invariance property of copulas. The copula remains constant even when individual distributions (marginals1) change, allowing analysts to adapt models without affecting the underlying dependency structure.
A copula describes the dependence structure between variables in terms of their relative ranks rather than their actual values or specific marginal distributions. The idea is to decouple the modeling of the marginals, which represent the individual behaviors of variables, from the dependence structure captured by the copula.
When the marginals change but their ranks remain similar , the copula can theoretically remain constant. For example, transforming a normal distribution to a log-normal distribution might
alter the marginal shape but preserve the rank order of the data. In such cases, the dependence structure described by the copula does not necessarily change, as it focuses on how the variables
co-move on a relative scale.
However, if the change in marginals significantly affects the rank order or relative behavior of the variables, then the dependence structure can be affected as well. This happens when the transformation of the marginals induces different relative behaviors between variables that were not captured in the original copula.
In practice, analysts use copulas by first fitting the copula to the ranked data of the variables, assuming that this dependence structure is fixed. Different marginal distributions can then be applied while keeping the same copula to maintain consistency.
This approach allows for flexibility in changing the marginals without directly modifying how the variables are assumed to co-move.
However, there are limitations to this assumption. If the marginal changes are extreme or induce significant changes in the rank correlation, the copula may no longer accurately represent the
dependence structure. Therefore, while the copula framework provides a way to change marginals without altering the perceived dependence, significant changes in the marginals can impact the true
dependence, particularly if they affect the rank order or joint behavior of the variables.
Suppose we have two financial assets X and Y with correlated returns. Assume \( X \) follows a normal distribution and \( Y \) an exponential distribution. A Clayton copula3 is chosen to model their dependency.
\[ C(u, v; \theta) = (u^{-\theta} + v^{-\theta} - 1)^{-1/\theta}, \quad \theta > 0 \]
According to Sklar's Theorem, we can construct their joint distribution function \( F(x, y) \) using the Clayton copula and the marginal distributions. If it's later found that \( X \) actually follows a log-normal distribution, only the marginal for \( X \) needs to be updated. The Clayton copula capturing the dependency between \( X \) and \( Y \) remains valid.
The applications of Sklar's Theorem are vast, particularly in finance where modeling the joint movements of asset returns is crucial. Copulas are extensively used in pricing multi-asset derivatives, risk management, and portfolio optimization.
Notes:
1 Marginals, in statistics, refer to the individual distributions of components within a multivariate distribution. They describe the probability distribution of each variable independently, ignoring the presence or influence of other variables in the dataset.
2 The word "copula" originates from Latin, where it means "a link" or "a bond."
3 The Clayton copula is a type of copula particularly good at capturing asymmetric tail dependence, meaning it can effectively model situations where extreme values in one variable are likely to be associated with extreme values in another.

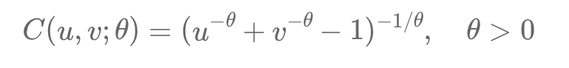
Écrire commentaire