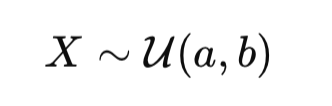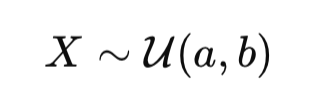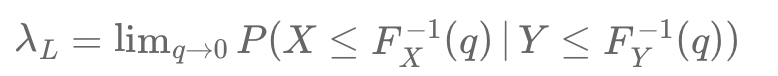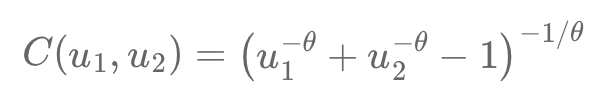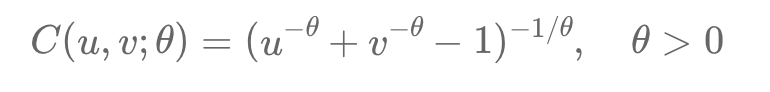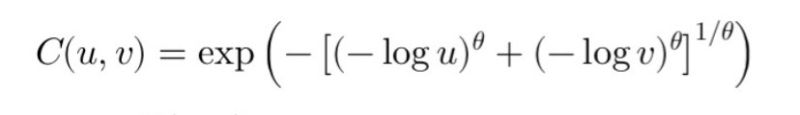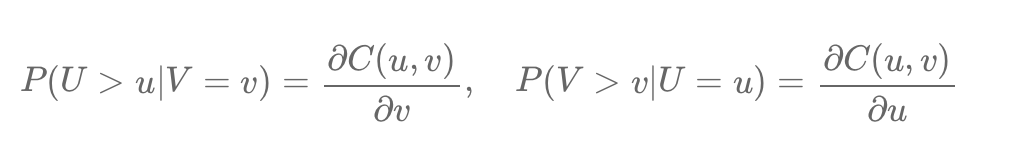Mathematical Principles and Quantitative Finance · 30. septembre 2024
Copulas help model dependencies between variables separately from their behaviors, crucial for finance's complex relationships. For example, Alice and Bob’s race times show dependency when transformed into uniform variables using cumulative distribution functions (CDFs). The Clayton copula captures asymmetric dependence, especially in lower tail risks, using the formula:
C(u1, u2) = (u1^(-θ) + u2^(-θ) - 1)^(-1/θ).
Mathematical Principles and Quantitative Finance · 29. juin 2024
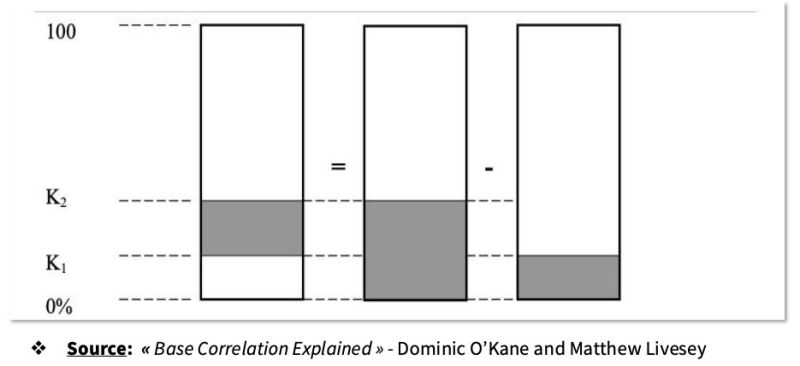
Collateralized Debt Obligations (CDOs) bundle debts into tranches with varying risk levels and returns. Correlation between these tranches is crucial as it affects their performance. Compound correlation assesses tranches independently, which can lead to incomplete risk profiles and mispricing. In contrast, base correlation, centered on the equity tranche which absorbs losses first, provides a more holistic view by considering inter-tranche dependencies, ensuring more accurate risk assessment.
Mathematical Principles and Quantitative Finance · 09. février 2024
Sklar's Theorem, a pivotal concept since 1959, separates the modeling of individual behaviors and dependencies in multivariate analysis, reshaping risk management and probabilistic modeling. It states that any multivariate distribution can be expressed via a copula linking its univariate marginal distributions. This theorem allows the copula to remain constant despite changes in individual distributions, enabling flexible and accurate modeling of complex dependencies.
Mathematical Principles and Quantitative Finance · 07. février 2024
Explore the hypercube's critical role in CDO risk modeling within quantitative finance. A hypercube extends a 2D square or 3D cube into an N-dimensional space, each axis representing a financial asset's cumulative distribution in copula functions. It's pivotal for visualizing complex dependencies in a CDO, where each axis indicates the default probability of different assets.
Mathematical Principles and Quantitative Finance · 05. janvier 2024
Discover the role of copulas in statistics, crucial for analyzing relationships between multiple variables in multivariate analysis. Copulas uniquely capture dependence structures, distinct from individual distributions. Focusing on the Gumbel copula, known for modeling tail dependencies in finance, we explore its effectiveness in assessing risks, like joint defaults in CDOs.
Principes mathématiques et applications en finance · 30. octobre 2023
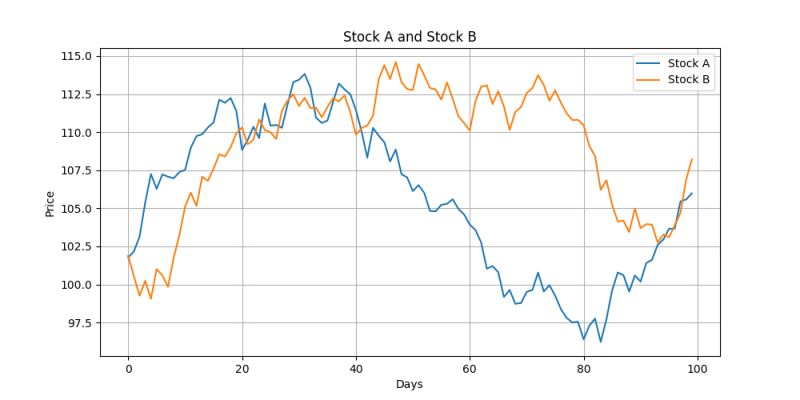
Unlock pairs trading with Copulas. Learn to analyze stocks like A & B, leveraging marginal & conditional distributions for strategic trades. Copulas link these distributions, revealing asset dependencies for optimized profitability & risk mitigation. Simple, insightful, actionable. #PairsTrading #Copula
Mathematical Principles and Quantitative Finance · 30. septembre 2023
Unlock pairs trading with Copulas. Learn to analyze stocks like A & B, leveraging marginal & conditional distributions for strategic trades. Copulas link these distributions, revealing asset dependencies for optimized profitability & risk mitigation. Simple, insightful, actionable. #PairsTrading #Copula