Stochastic processes are mathematical models used to describe systems that evolve randomly over time. They are widely applied in fields such as physics, biology, and finance to capture uncertainty and randomness in dynamic systems. A fundamental example is the Wiener process1, also known as Brownian motion, which models continuous and unpredictable movements. Characterized by independent increments and a Gaussian distribution, it serves as the foundation for modern stochastic calculus. In this context, we explore the interaction between a Wiener process and its integral: \[ \int_0^t W_s \, ds \] This interaction defines a new stochastic process with unique properties, blending instantaneous randomness with accumulated historical effects. Such combinations are essential for modeling systems where both present values and past behaviors influence outcomes, making them powerful tools for analyzing complex financial and physical systems.
The nature of the product
The process defined by the product \( W_t \cdot \int_0^t W_s \, ds \) is inherently nonlinear. In stochastic calculus, studying nonlinear transformations of stochastic processes often requires advanced techniques such as Itô's lemma2, which enables differentiation and integration of such processes.
\[ X_t = W_t \cdot \int_0^t W_s \, ds \]
This product creates a new stochastic process that inherits randomness from the Wiener process. Its behavior is more intricate than that of either \( W_t \) or \( \int_0^t W_s \, ds \) considered independently. The complexity arises from combining the current value of \( W_t \) with its accumulated history, making it well-suited for systems where both present and past states influence outcomes.
Quadratic covariation and interaction
The concept of quadratic covariation3 provides insights into the relationship between \( W_t \) and \( \int_0^t W_s \, ds \). Quadratic covariation measures how two stochastic processes interact through their joint fluctuations, revealing nonlinear dependencies that cannot be captured by simple linear relationships.
\[ [W_t, \int_0^t W_s \, ds]_t \]
For the product \( W_t \cdot \int_0^t W_s \, ds \), quadratic covariation highlights how the instantaneous variations of \( W_t \) influence the cumulative behavior captured by its integral. This property is particularly useful in pricing path-dependent instruments such as Asian options4, where historical averages play a central role in valuation.
Memoryless property versus accumulated history
The Wiener process, or Brownian motion, is well-known for its memoryless property. Its increments are independent, meaning that for any \( s < t \), the increment \( W_t - W_s \) depends only on the time interval and not on the process’s past trajectory.
\[ E[W_t - W_s] = 0, \quad Var(W_t - W_s) = t - s \]
In contrast, the integral \( \int_0^t W_s \, ds \) aggregates past values of the Wiener process, capturing historical information. Unlike \( W_t \), which is memoryless, this integral retains a record of past behavior, making it fundamentally different in nature.
By combining \( W_t \) with its integral, we construct a process that bridges memoryless behavior with historical dependence. This interaction is especially relevant for modeling systems where the present state dynamically depends on the accumulated effects of past events, a property frequently encountered in finance.
Applications in financial mathematics
The product \( W_t \cdot \int_0^t W_s \, ds \) plays a central role in modeling path-dependent financial instruments. A notable example is Asian options, whose payoff depends on the average price of the underlying asset over time, reflecting its historical performance.
\[ A_T = \frac{1}{T} \int_0^T S_t \, dt \]
Understanding the interaction between present and past behavior in stochastic processes is essential for evaluating price dynamics and risk exposure in such instruments. Tools like the Jacobian matrix and quadratic covariation enable a more accurate representation of dependencies, enhancing modeling and pricing strategies in finance.
1. Wiener Process: Also known as Brownian motion, a stochastic process with independent increments, zero mean, and variance proportional to time.
2. Itô's Lemma: A fundamental result in stochastic calculus used to calculate the differential of functions involving stochastic processes.
3. Quadratic Covariation: A measure of how two stochastic processes interact through their joint fluctuations, especially useful for processes involving non-linear relationships.
4. Asian Options: Exotic options where the payoff depends on the average price of the underlying asset over a specific time period, making them path-dependent.
🎓 Recommended Training: The Fundamentals of Quantitative Finance
Discover the essential concepts of quantitative finance, explore applied mathematical models, and learn how to use them for risk management and asset valuation.
Explore the Training

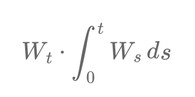
Écrire commentaire