Brownian motion, a cornerstone concept in stochastic processes, illustrates a world of constant, random movement. Imagine a particle wandering unpredictably, with each step independent of the last. The resulting path is continuous yet non-differentiable at every point, making it one of the most intriguing phenomena in mathematics.
A continuous function is differentiable at a specific time \( t \) if its derivative can be determined by analyzing how the function behaves as it approaches \( t \). Differentiability implies a degree of predictability: the past behavior of the function provides insights into its future evolution. However, Brownian motion defies this notion. At any given point \( t \), its value is completely independent of the values preceding it, making it fundamentally unpredictable.
This unpredictability is encoded in the very definition of Brownian motion. If \( B_t \) represents the value of a Brownian motion at time \( t \), then the increments \( B_{t+s} - B_t \) are independent and follow a normal distribution:
\[ B_{t+s} - B_t \sim N(0, s). \]
This property, combined with its continuity, leads to the counterintuitive fact that the path of Brownian motion is non-differentiable everywhere. This non-differentiability is not a flaw but a feature that captures the essence of randomness.
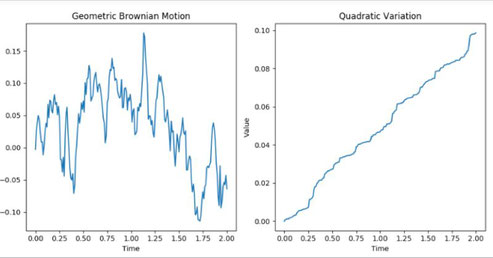
The roughness of Brownian motion paths can be quantified using a concept called quadratic variation. Unlike classical measures that smooth out irregularities, quadratic variation embraces and measures this roughness. For a Brownian motion \( B_t \), the quadratic variation over an interval \([0, t]\) is defined as:
\[ [B]_t = \lim_{n \to \infty} \sum_{i=1}^{n} (B_{t_i} - B_{t_{i-1}})^2, \]
where \(\{t_i\}\) represents a partition of the interval. Remarkably, the quadratic variation 1 of Brownian motion increases linearly with time:
\[ [B]_t = t. \]
This linearity reflects the accumulation of randomness over time, with every increment adding to the overall variability of the path.
In financial modeling, the properties of Brownian motion find extensive applications, particularly in the study of asset prices. Geometric Brownian Motion (GBM), a popular model for stock prices, extends Brownian motion by incorporating a drift component and a volatility term. The evolution of a stock price \( S_t \) under GBM is described by the stochastic differential equation:
\[ dS_t = \mu S_t dt + \sigma S_t dB_t, \]
where \( \mu \) is the drift rate, \( \sigma \) represents volatility, and \( dB_t \) is the Brownian motion increment. The quadratic variation of \( B_t \) plays a crucial role in capturing the randomness inherent in financial markets. It directly influences the volatility term, offering insights into market behavior and risk.
The linear relationship between quadratic variation and time in Brownian motion translates into a measure of market uncertainty. In GBM, this property helps quantify volatility, a critical
parameter for pricing derivatives and assessing financial risk.
The non-differentiability of Brownian motion reminds us that while financial markets can be modeled mathematically, their intrinsic randomness and unpredictability remain ever-present. This characteristic is a driving force behind the development of sophisticated tools in quantitative finance.
1 Quadratic variation measures the cumulative squared increments of a stochastic process, offering a way to quantify its "roughness" over a given time interval.

Écrire commentaire