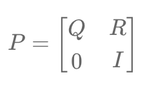
Imagine playing a board game where you move between different states based on dice rolls. Each space on the board represents a state, and you transition between states based on the dice outcome – this is the basic idea of a "Markov chain."
Now, imagine some spaces on the board are special rooms with no way out once you enter them. These special rooms are called "absorbing states." Once you step into one, you're stuck there indefinitely.
In the context of the dice game, the "absorbing Markov chain" is a version of the game where certain spaces act like traps.
Imagine you're analyzing a mix of stocks in your investment portfolio. The stocks are divided into three categories: "Tech," "Energy," and "Consumer Goods." The movements between these categories depend on market trends and other financial factors.
Now, let's assume that stocks in "Tech" and "Energy" can transition between each other based on market conditions. But stocks categorized as "Consumer Goods" have an interesting trait – when they perform well, they tend to remain in that state due to steady consumer demand.
- State 1: "Tech" stocks
- State 2: "Energy" stocks
- State 3: "Consumer Goods" stocks
"Consumer Goods" stocks are the absorbing state here. Once stocks end up in this state, they usually stick around for a significant period due to consumer behavior. It's like a trend that maintains itself.
The absorbing Markov chain helps you understand the probabilities of stocks transitioning between these states and eventually landing in the absorbing state of "Consumer Goods." Once they're there, you know they'll likely stay for some time due to the absorbing property.
In an absorbing Markov chain, the numbers linked to the edges of the graph represent transition probabilities. These probabilities indicate how likely it is for the system to move from one state (node) to another state (node).
- ('Tech', 'Energy'): 0.4. This line signifies a transition probability of 40% from state 'Tech' to state 'Energy'.
- ('Energy', 'Tech'): 0.3. In this case, the probability of transitioning from 'Energy' to 'Tech' is a 30% chance of making this transition.
- ('Tech', 'Consumer Goods'): 0.2. This line represents a transition probability of 20% from 'Tech' to the absorbing state 'Consumer Goods'.
- ('Energy', 'Consumer Goods'): 0.1. Similarly, the probability of transitioning from 'Energy' to 'Consumer Goods' is 10%.
These transition probabilities define how the system moves from one state to another. They are crucial in understanding the behavior of the Markov chain and how it evolves over time. The probabilities help you quantify the likelihood of transitioning between states, and they drive the dynamics of the system represented by the absorbing Markov chain.
Write a comment