L’intervalle de confiance en termes simples - Finance Tutoring
En finance, les décisions reposent souvent sur des prévisions issues de données statistiques. Cependant, ces prévisions comportent un niveau d'incertitude qu'il est essentiel de quantifier pour prendre des décisions éclairées. Les intervalles de confiance sont au cœur de ce contexte, fournissant une plage dans laquelle un paramètre estimé, comme un rendement moyen, est susceptible de se trouver avec une probabilité donnée.
Définition
Un intervalle de confiance est une plage autour d'une estimation ponctuelle qui indique où le véritable paramètre de la population (par exemple, la moyenne) a une forte probabilité de se trouver. Par exemple, un intervalle de confiance à 95 % signifie que si l'échantillonnage était répété plusieurs fois, 95 % des intervalles calculés contiendraient le paramètre réel.
L'intervalle de confiance est calculé à l'aide de la formule suivante :
\[ \text{Intervalle de Confiance} = \bar{x} \pm z \cdot \text{ES}, \]
où :
- \( z \) est la valeur critique associée au niveau de confiance (par exemple, 1,96 pour 95 %),
- \( \text{ES} \) (Erreur Standard) est calculée comme :
\[ \text{ES} = \frac{s}{\sqrt{n}}, \]
avec \( s \) étant l'écart-type des données et \( n \) la taille de l'échantillon.
Rôle de l'Intervalle de Confiance
Les intervalles de confiance sont essentiels en finance pour plusieurs raisons :
- 1. Mesurer l'incertitude : Ils permettent d'estimer le degré d'incertitude autour d'un paramètre financier comme un rendement moyen, un taux d'intérêt ou une volatilité.
- 2. Prise de décision : En fournissant une plage probable, ils aident les gestionnaires de risques ou les investisseurs à prendre des décisions en tenant compte des scénarios optimistes et pessimistes.
- 3. Comparaison des performances : Les intervalles de confiance sont utilisés pour déterminer si les différences entre deux actifs financiers (par exemple, deux portefeuilles) sont statistiquement significatives.
Pourquoi l'Erreur Standard est-elle Importante ?
L'erreur standard mesure la variabilité des moyennes échantillonnales autour de la moyenne réelle de la population. Elle dépend de :
- L'écart-type (\( s \)) : Une plus grande dispersion des données entraîne une erreur standard plus élevée.
- La taille de l'échantillon (\( n \)) : Un échantillon plus grand réduit l'erreur standard (car l'incertitude moyenne diminue avec davantage de données).
Avantages et Inconvénients d'un Intervalle Large
Un intervalle de confiance peut être large ou étroit selon la variabilité des données, la taille de l'échantillon et le niveau de confiance choisi. Voici les implications d'un intervalle large :
Avantages :
- 1. Fiabilité accrue : Un intervalle large reflète une probabilité plus élevée d'inclure le paramètre réel, ce qui est essentiel pour des analyses prudentes comme les tests de résistance ou les scénarios de crise.
- 2. Gestion des incertitudes : Il prend pleinement en compte les incertitudes liées à la volatilité et à la dispersion des données.
Inconvénients :
- 1. Précision réduite : Un intervalle large indique une grande dispersion des données (\( s \)) ou un petit échantillon (\( n \)), signifiant que le paramètre estimé peut s'écarter fortement de la moyenne réelle.
- 2. Difficulté de prise de décision : En finance, un intervalle très large, comme une prévision de rendement entre -10 % et +20 %, est difficile à interpréter pour guider une stratégie.
Illustration avec un Exemple Financier
Supposons que vous analysiez un portefeuille d'actions avec un rendement moyen (\( \bar{x} \)) de 5 %, un écart-type (\( s \)) de 15 %, et une taille d'échantillon (\( n \)) de 30 observations. L'erreur standard est :
\[ \text{ES} = \frac{15}{\sqrt{30}} \approx 2,74. \]
Pour un intervalle de confiance de 95 % (\( z = 1,96 \)) :
\[ \text{Intervalle de Confiance} = 5 \pm 1,96 \cdot 2,74 \approx [-0,37\%, 10,37\%]. \]
Cet intervalle indique une probabilité de 95 % que le rendement moyen réel se situe entre -0,37 % et 10,37 %. Bien que fiable, cette plage est trop large pour permettre une prise de décision précise, illustrant les limites d'un intervalle large.
Les intervalles de confiance sont des outils puissants pour évaluer l'incertitude et guider les décisions stratégiques en finance. Cependant, un intervalle large, bien qu'il augmente la fiabilité, réduit la précision et complique l'interprétation. Trouver un équilibre entre fiabilité et précision est crucial, cet équilibre dépendant de la taille de l'échantillon, de la volatilité des données, et du niveau de confiance souhaité.

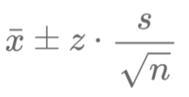
Écrire commentaire