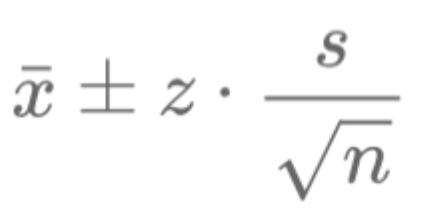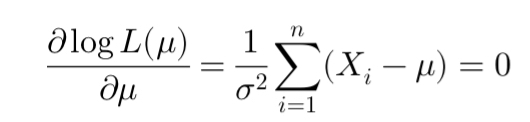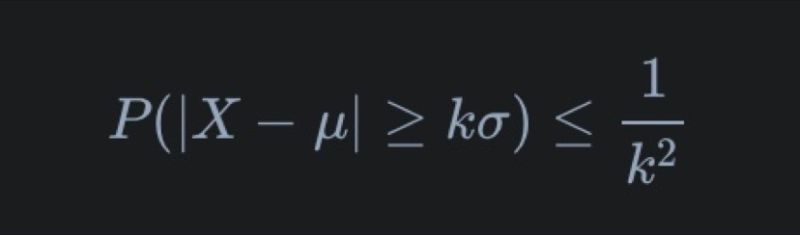Statistiques · 07. décembre 2024
Les intervalles de confiance sont des outils essentiels en finance, permettant de quantifier l'incertitude dans les estimations statistiques telles que les rendements moyens, les taux d'intérêt ou la volatilité. Ils fournissent une plage dans laquelle le véritable paramètre de la population est susceptible de se trouver, facilitant ainsi la prise de décision et les comparaisons de performances.
Principes mathématiques et applications en finance · 12. octobre 2024
L'estimation par maximum de vraisemblance (EMV) est une méthode statistique utilisée pour estimer les paramètres d’un modèle à partir de données observées. Elle consiste à trouver les valeurs des paramètres qui maximisent la probabilité d’observer ces données. L'EMV est couramment utilisée en finance, par exemple pour estimer des mesures de risque comme la Value-at-Risk et l’Expected Shortfall en ajustant des modèles comme la distribution de Pareto généralisée aux événements extrêmes.
Mathematical Principles and Quantitative Finance · 11. novembre 2023
Chebyshev's inequality, vital in probability theory and finance, estimates the probability of a variable deviating from its mean by more than k standard deviations, capped at 1/k². Useful in finance for risk analysis and asset allocation, it applies to various distributions without needing a normal distribution assumption. However, it may overestimate extreme outcomes, leading to conservative strategies. #ChebyshevsInequality #QuantitativeFinance #RiskManagement #FinancialAnalysis
Statistiques · 01. octobre 2023
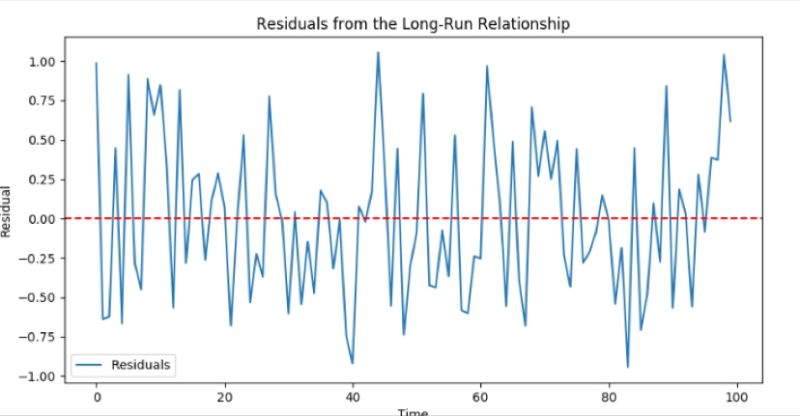
Explore cointegration in finance with our easy guide. Learn pairs trading & hedging with assets that move together long-term, offsetting risks. Master the Engle-Granger method & visualize asset correlation for informed investment. Updated, mobile-optimized content for every investor. #Cointegration #TradingStrategy