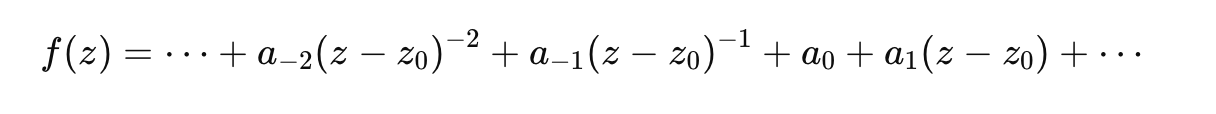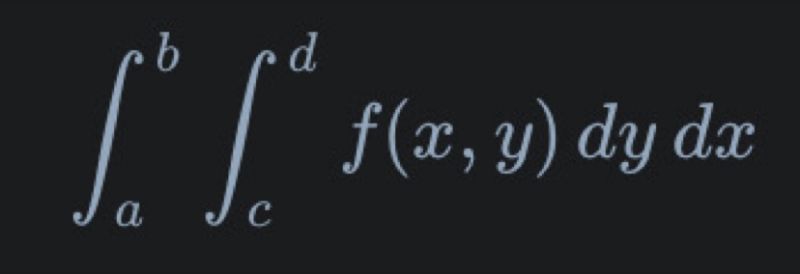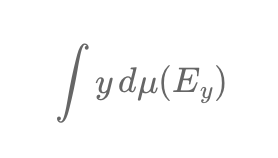Mathematical Principles and Quantitative Finance · 03. octobre 2024
Laurent series, extensions of Taylor series, model functions around singularities and are essential in quantitative finance for asset and option valuation. They converge in an annulus, unlike Taylor series that converge within a disk.
Mathematical Principles and Quantitative Finance · 11. mai 2024
Double integrals are vital in option pricing, enabling analysis of volume under surfaces relevant to financial models. They integrate over two-dimensional areas, representing volume under a surface defined by \( f(x, y) \) over region \( R \). They're particularly useful for complex options with dependencies on multiple correlated variables, like Asian or basket options. In Black-Scholes modeling, risk-neutral prices involve integrating payoff over probability density functions.
Mathematical Principles and Quantitative Finance · 12. septembre 2023
The Lebesgue integral offers a powerful approach for tackling functions with numerous discontinuities, where traditional Riemann methods fail. This makes it invaluable in quantitative finance, enabling the modeling of sudden market jumps and refining risk management. Lebesgue-inspired techniques enhance financial models, capturing real-world market volatility.
11. septembre 2023
Understanding Fractional Differentiation:
Think of it as measuring temperature now vs. its trend over time. In finance:
1. Asset Price Models: Traditional views vs. Fractional differentiation's long-term memory, e.g., Fractional Brownian Motion.
2. Risk Management: Models like VaR become more accurate.
3. Options Pricing: Enhanced with past price trends.
4. Interest Rates: Captures past rate shifts, refining models.
It bridges current data with past patterns, vital in quantitative finance.
Mathematical Principles and Quantitative Finance · 24. juin 2023
Integration in finance is like piecing together a puzzle of market changes. Instead of analyzing each tiny change individually, integration sums it all up, giving a clearer overall picture. Think of predicting a concert ticket price: integration takes into account past prices, demand, and unexpected surges in popularity. It simplifies the complex financial landscape by aggregating vast data, helping experts make informed decisions. #FinancialIntegrationExplained