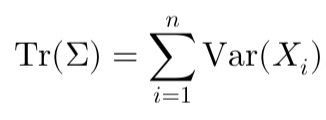Mathematical Principles and Quantitative Finance · 29. septembre 2024
In finance, matrices are essential for organizing and analyzing data like asset returns, correlations, and risks. They allow for compact manipulation of complex relationships, aiding in portfolio analysis, derivative pricing, and investment optimization.
A key matrix is the covariance matrix, Σ (Sigma), which captures how asset returns vary individually and with each other.