Une swaption est une option qui donne à son détenteur le droit, mais non l'obligation, de conclure un swap de taux d'intérêt à une date future. Il existe deux types de swaptions :
- Une payer swaption permet au détenteur de payer un taux fixe et de recevoir un taux variable. Elle s'apparente à une option d'achat sur les taux d'intérêt, avantageuse en cas de hausse des taux.
- Une receiver swaption permet au détenteur de recevoir un taux fixe et de payer un taux variable. Elle est similaire à une option de vente sur les taux d'intérêt, avantageuse lorsque les taux baissent.
- Une entreprise peut acheter une payer swaption pour se protéger contre une hausse des coûts d'emprunt,
- Un titulaire de prêt hypothécaire pourrait acheter une receiver swaption pour se protéger contre une baisse des taux.
La valeur d'une swaption est dérivée des flux de trésorerie attendus du swap sous-jacent, actualisés au présent en utilisant la courbe zéro-coupon.
Le taux de swap à terme est le taux fixe convenu aujourd'hui pour un swap qui commencera à une date future. Il représente le taux auquel le marché s'attend à ce que les paiements fixes d'un swap soient échangés contre des paiements variables à l'avenir, équivalent au prix d’un IRS débutant dans le futur.
La courbe zéro-coupon, qui représente les rendements des obligations zéro-coupon obtenus par "bootstrapping" à partir des prix de divers titres sans risque de différentes maturités, est utilisée pour actualiser les flux de trésorerie futurs à leur valeur actuelle. La courbe zéro-coupon fournit également les taux à terme nécessaires pour évaluer les swaps dans un environnement sans arbitrage.
La volatilité implicite est également utilisée pour la tarification des swaptions, car elle capture les attentes du marché concernant les mouvements futurs des taux d’intérêt et influence directement la prime de la swaption.
Une méthode de valorisation des swaptions est le modèle de Black, qui utilise les formules suivantes : \[ PV_{payer}(t) = NA[S \cdot \Phi(d_1) - K \cdot \Phi(d_2)] \] \[ PV_{receiver}(t) = NA[K \cdot \Phi(-d_2) - S \cdot \Phi(-d_1)] \] Où :
- \( N \) : montant notionnel principal
- \( A \) : facteur d'annuité, la valeur actuelle de la jambe fixe du swap
- \( S \) : taux de swap à terme
- \( K \) : taux d'exercice de la swaption
- \( \Phi \) : fonction de distribution normale standard cumulative
- \( d_1 = \frac{\ln(S/K) + (\sigma^2 / 2) \cdot T}{\sigma \sqrt{T}} \)
- \( d_2 = d_1 - \sigma \sqrt{T} \)
Prenons l'exemple suivant pour valoriser une payer swaption :
- Notionnel (\( N \)) : 10 000 000 $
- Maturité de la swaption (\( T \)) : 1 an
- Durée du swap sous-jacent : 5 ans
- Taux d'exercice (\( K \)) : 3 %
- Taux de swap à terme (\( S \)) : 3,5 %
- Volatilité implicite (\( \sigma \)) : 20 %
- Facteur d'annuité (\( A \)) : environ 4,25 ans
- Facteurs d’actualisation (\( D_1 = 0{,}95, D_5 = 0{,}80 \))
Montant de la prime pour cette payer swaption : \[ PV_{payer} = NA[S \cdot \Phi(d_1) - K \cdot \Phi(d_2)] \\ = 10\,000\,000 \cdot 4{,}25 \cdot [(0{,}035 \cdot 0{,}8078) - (0{,}03 \cdot 0{,}7486)] \\ = 247\,362{,}50\,\$ \]
Notes
- 1. Le taux de swap à terme est aussi appelé taux FRA dans d'autres contextes.
- 2. Le facteur d'annuité représente la valeur actuelle de 1 unité de notionnel versée annuellement sur la durée du swap, actualisée via la courbe zéro.
Une swaption est une option qui donne à son détenteur le droit, mais non l'obligation, de conclure un swap de taux d'intérêt à une date future. Il existe deux types de swaptions :
- Un payer swaption permet au détenteur de payer un taux fixe et de recevoir un taux variable. Elle s'apparente à une option d'achat sur les taux d'intérêt, avantageuse en cas de hausse des taux.
- Un receiver swaption permet au détenteur de recevoir un taux fixe et de payer un taux variable. Elle est similaire à une option de vente sur les taux d'intérêt, avantageuse lorsque les taux baissent.
Les swaptions sont utilisées pour se couvrir contre les risques de taux d'intérêt ou à des fins spéculatives.
Par exemple, une entreprise peut acheter une payer swaption pour se protéger contre une hausse des coûts d'emprunt, tandis qu'un titulaire de prêt hypothécaire pourrait acheter une receiver swaption pour se protéger contre une baisse des taux.
La valeur d'une swaption est dérivée des flux de trésorerie attendus du swap sous-jacent, actualisés au présent en utilisant la courbe zéro-coupon. Le taux de swap à terme et la volatilité implicite sont des éléments clés de l'évaluation.
- Le taux de swap à terme est le taux fixe convenu aujourd'hui pour un swap qui commencera à une date future. Il représente le taux auquel le marché s'attend à ce que les paiements fixes d'un swap soient échangés contre des paiements variables à l'avenir, équivalent au prix d'un IRS débutant dans le futur.
- La courbe zéro-coupon, qui représente les rendements des obligations zéro-coupon obtenus par "bootstrapping" à partir des prix de divers titres sans risque de différentes maturités, est utilisée pour actualiser les flux de trésorerie futurs à leur valeur actuelle.
La courbe zéro-coupon fournit également les taux à terme nécessaires pour évaluer les swaps dans un environnement sans arbitrage.
- La volatilité implicite est également utilisée pour la tarification des swaptions, car elle capture les attentes du marché concernant les mouvements futurs des taux d'intérêt et influence directement la prime de la swaption.
Une méthode de valorisation des swaptions est le modèle de Black, qui utilise les formules suivantes:
- PV_payer(t) = NA[S * Φ(d1) - K * Φ(d2)]
- PV_receiver(t) = NA[K * Φ(-d2) - S * Φ(-d1)
Où :
- N = montant notionnel principal
- A = facteur d'annuité, la valeur actuelle de la jambe fixe du swap
- S = taux de swap à terme
- K = taux d'exercice de la swaption
- Φ = fonction de distribution normale standard cumulative
- d1 = [ln(S/K) + (σ^2 / 2) * T] / (σ * sqrt(T))
- d2 = d1 - σ * sqrt(T)
Prenons l'exemple suivant pour valoriser une payer swaption :
- Notionnel (N) : 10 000 000 $
- Maturité de la swaption (T) : 1 an
- Durée du swap sous-jacent : 5 ans
- Taux d'exercice (K) : 3 %
- Taux de swap à terme (S) : 3,5 %
- Volatilité implicite (σ) : 20 %
- Facteur d'annuité (A) : Environ 4,25 ans
- Facteurs d'actualisation (D1 = 0,95, D5 = 0,80)
Soit:
- ln(3,5 % / 3 %) = ln(1,1667) ≈ 0,154
- σ^2 / 2 = 0,02
- d1 = (0,154 + 0,02) / 0,2 = 0,87
- d2 = 0,87 - 0,2 = 0,67
- Φ(0,87) ≈ 0,8078
- Φ(0,67) ≈ 0,7486
PV_payer = NA[S * Φ(d1) - K * Φ(d2)] = 10 000 000 * 4,25 * [(0,035 * 0,8078) - (0,03 * 0,7486)] = 247 362,50 $.
🎓 Formation recommandée : Les fondamentaux des options
Découvrez le rôle et le fonctionnement des options, leur utilisation et sachez interpréter les Grecques
Découvrir la formation

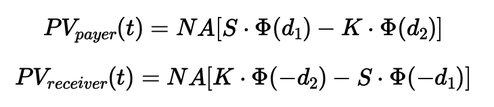
Écrire commentaire