Imagine trying to understand all possible events in a system, much like analyzing the possible outcomes of drawing cards from a deck. A sigma-algebra provides the necessary structure to assign probabilities to various events within this system, ensuring a logical and consistent framework for decision-making.
Defining Probabilities as Events
An event is essentially a subset of possible outcomes. For instance, if you’re interested in “drawing an Ace” from a deck, the event is the set containing all Aces in that deck. Mathematically, events are part of a broader set, called the sample space (\( \Omega \)), which represents all possible outcomes.
\[ P(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}} \]
Let \( A \) be the event “drawing an Ace.” Then \( A \) is a subset of \( \Omega \) (the entire deck), and we assign a probability to this event.
Combining Events
You might want to calculate probabilities for combined events, such as “drawing an Ace or a King.” This involves combining the individual events of drawing an Ace (\( A \)) and drawing a King (\( B \)). A probability model should handle such unions of events effectively.
\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]
where \( P(A \cap B) \) is the probability of both \( A \) and \( B \) happening simultaneously. In this example, the probability of drawing a card that is both an Ace and a King is 0, as they are mutually exclusive.
Complementary Events
It’s important to also consider the complement of an event, or what happens if the event does not occur. For example, if the event is drawing an Ace (\( A \)), its complement (\( A^c \)) is “not drawing an Ace.” The rules of probability require assigning a value to this complementary event:
\[ P(A^c) = 1 - P(A) \]
This follows because the probability of either an event or its complement must equal 1 (the total probability).
Key Rules of Sigma-Algebra
\[ P(\Omega) = 1 \]
The entire sample space \( \Omega \) is always considered, and its probability equals 1.
If \( A \) and \( B \) are events in the sigma-algebra, then their union \( A \cup B \) is also in the sigma-algebra, satisfying closure under union.
For any event \( A \) in the sigma-algebra, its complement \( A^c \) is also in the sigma-algebra, satisfying closure under complement.
Why Sigma-Algebra Matters in Finance
In finance, the events we’re interested in are far more complex than drawing cards. These events could be movements of stock prices, interest rate changes, or economic indicators. The sigma-algebra provides a structured way to assign probabilities consistently to such complex and intertwined events, ensuring that calculations and models remain logical and coherent.
Consistency in Complex Markets: Financial markets involve numerous possible events and outcomes, often interdependent. A sigma-algebra ensures that probabilities are assigned in a way that remains consistent across all possible scenarios.
Dynamic Information Over Time: Financial information evolves dynamically. As time progresses, new information about the market affects probabilities. The sigma-algebra evolves to incorporate this information, helping model future scenarios based on present knowledge. This is especially relevant when considering the path that a stock price might take over time or when analyzing sequences of events.
In practice, we often work with a sequence of sigma-algebras over time, represented as a filtration:
\[ \mathcal{F}_t \subseteq \mathcal{F}_{t+1} \subseteq \dots \subseteq \mathcal{F}_T \]
Each \( \mathcal{F}_t \) represents the information available up to time \( t \), and the sigma-algebra grows as more information is revealed over time.
A sigma-algebra is a mathematical structure that organizes events and their probabilities in a way that allows consistent, meaningful calculations. This structure is essential in finance to ensure that models remain consistent as they handle complex events over time. Without such a structure, financial models could become illogical, contradictory, or chaotic.
Key Takeaways:
1. Events & Probabilities: Events are subsets of a sample space (Ω). Probability of event A: P(A) = (favorable outcomes) / (total outcomes).
2. Combining Events: For combined events like “Ace or King,” use the union formula: P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
3. Complementary Events: Complement (A^c) represents “not A.” Probability: P(A^c) = 1 - P(A).
4. Sigma-Algebra Rules:
• Whole Set: Full sample space Ω has P(Ω) = 1.
• Union: The union of any events (A ∪ B) is part of the sigma-algebra.
• Complement: The complement of any event (A^c) is also included.
5. Finance Application: Sigma-algebra structures probabilities for complex, evolving financial events. It evolves over time (filtration: F_t ⊆ F_{t+1} ⊆ … ⊆ F_T) to reflect changing information.
🎓 Recommended Training: The Fundamentals of Quantitative Finance
Discover the essential concepts of quantitative finance, explore applied mathematical models, and learn how to use them for risk management and asset valuation.
Explore the Training

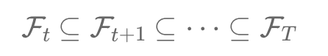
Écrire commentaire