The Characteristic Function: An Overview
The characteristic function of a real random variable \( X \) encodes all the information about the probability distribution of \( X \). In other words, the characteristic function uniquely determines the distribution of \( X \).
The characteristic function \( \phi_X(u) \) of a random variable \( X \) is defined as:
\[ \phi_X(u) = \mathbb{E}[\exp(i \cdot u \cdot X)] \]
Here:
- \( \mathbb{E}[.] \): Represents the expectation (or mean) with respect to the distribution of \( X \).
- \( u \): Any real number acting as a "frequency" parameter in the context of Fourier analysis.
- \( i \): The imaginary unit (\( i^2 = -1 \)).
The characteristic function takes each possible value of \( u \) and calculates the mean of the complex exponential associated with the random variable \( X \). In this context, \( u \) acts as a parameter that "probes" or "transforms" the distribution of \( X \).
Why Use the Complex Exponential Function?
The complex exponential function \( \exp(i \cdot u \cdot X) \) plays a central role in the definition of the characteristic function. This choice is motivated by several reasons:
1. Connection to Fourier Analysis: The complex exponential function is fundamental in Fourier analysis, which provides a powerful way to analyze signals and probability distributions. By
transforming the distribution into the frequency domain, it becomes possible to study the structure and properties of the random variable \( X \) more effectively.
2. Unique Representation: The Fourier transform, which is based on the complex exponential function, is invertible. This ensures that the characteristic function uniquely determines the
probability distribution of \( X \). This bijective relationship is crucial for applications like recovering the probability density function (PDF) from the characteristic function.
3. Simplification of Mathematical Operations: The exponential function has convenient properties under differentiation and integration, making it easier to work with sums, products, and
convolutions of random variables. This is particularly useful when deriving moments or analyzing complex random systems.
4. Representation of Oscillatory Behavior : The complex exponential function combines real and imaginary components (\( e^{i \cdot u \cdot X} = \cos(u \cdot X) + i \sin(u \cdot X) \)).
This dual nature allows it to capture both amplitude and phase information, making it ideal for representing probability distributions in the frequency domain.
5. Analysis of Symmetry and Independence: The characteristic function provides insights into the symmetry and independence of random variables. For example, the characteristic function of
a symmetric random variable has specific symmetry properties that are directly tied to the use of the complex exponential function.
Link to the Probability Density Function
If the random variable \( X \) has a probability density function \( f_X(x) \) (1), then the characteristic function is linked to this density via the Fourier transform:
\[ \phi_X(u) = \int_{-\infty}^{+\infty} \exp(i \cdot u \cdot x) \cdot f_X(x) \, dx. \]
The density \( f_X(x) \) can be recovered from the characteristic function using the inverse Fourier transform:
\[ f_X(x) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \exp(-i \cdot u \cdot x) \cdot \phi_X(u) \, du. \]
This relationship illustrates how the characteristic function serves as a bridge between the time domain and the frequency domain in stochastic processes.
Moments and the Characteristic Function
The \( k \)-th moment of a random variable, if it exists, is defined as \( \mathbb{E}(X^k) \). For example, the expectation (or mean) of a random variable is its first moment, and the variance is its centered moment of order 2.
For a finite discrete random variable \( X \), the \( k \)-th moment is given by:
\[ m_k = \sum x_i^k \cdot P(X = x_i), \]
where the summation is over all possible values of \( X \). If \( X \) has a probability density function \( f \), the \( k \)-th moment is:
\[ m_k = \int_{\mathbb{R}} x^k \cdot f(x) \, dx. \]
By taking derivatives of \( \phi_X(u) \) around \( u = 0 \), we can systematically retrieve all the moments (mean, variance, skewness, etc.) without needing to integrate over the original probability density, simplifying the analysis.
1 Probability Density Function (PDF): A function \( f_X(x) \) that indicates the likelihood of a continuous random variable \( X \) taking specific values.

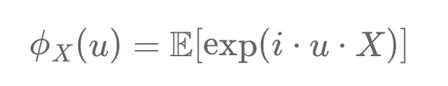
Écrire commentaire