Les fonctions indicatrices occupent une place fondamentale en mathématiques financières, car elles servent de conditions binaires pour l’évaluation des actifs risqués.
Elles permettent d’agir comme des interrupteurs dans les formules, incluant ou excluant certains termes en fonction du respect de conditions précises.
Par exemple, lors de l'évaluation de la valeur d'une obligation à coupon zéro dans un univers risque-neutre (*), nous tenons compte de la valeur actuelle attendue du paiement, actualisée au taux
sans risque. La formule intègre la fonction indicatrice pour tenir compte de la possibilité de défaut de l'émetteur.
La formule de sa valeur s'exprime comme suit :
E* [
exp(−∫ r(s) ds) * 1 {τ > T} ] de t à T
mathbb{E}^* left[ e^{-int_0^T r(s) , ds} cdot mathbb{1}_{ au > T} ight] ext{dét}_
Cette formule suppose que le paiement n'a lieu que si l'émetteur ne fait pas défaut avant l'échéance de l'obligation.
En partant de ce concept, considérons un scénario plus complexe où nous introduisons la possibilité de défaut avant l'échéance. La valeur d'une obligation à coupon zéro risquée est alors donnée
par la somme de deux composantes : l'une reflétant le scénario sans défaut et l'autre tenant compte de l'événement de défaut. La formule de pricing d'une obligation risquée, en tenant compte du
risque de défaut, est la suivante:
D(t, T) = E* [ exp(-∫ de t à T de r(s) ds) * 1 {τ > T} + exp(-∫ de t à τ de r(s) ds) * δ * 1 {t < τ ≤ T} ]
Ici, le premier terme à droite de l’équation représente la valeur en l'absence de défaut, tandis que le deuxième terme ajuste la valeur pour tenir compte de la possibilité de défaut avant
l'échéance, pondéré par le taux de recouvrement δ.
Cette application de la fonction indicatrice permet de modéliser les dynamiques complexes du prix obligations dans le cadre desquelles le risque de défaut est un facteur significatif.
(*) L’univers risque-neutre suppose qu'il n'y a pas d'opportunités d'arbitrage, ce qui signifie que tous les actifs sont évalués de telle manière qu'aucun profit sans
risque ne peut être réalisé à partir d’inefficiences de marché.

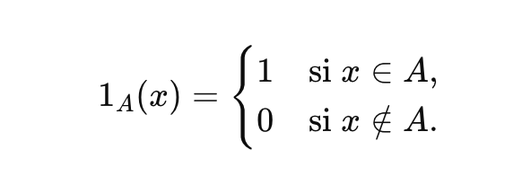
Écrire commentaire