Vous avez déjà eu l'impression que l'équation de Black-Scholes était une montagne trop difficile à gravir ? J'ai décomposé la dérivation étape par étape dans un document de 3 pages facile à suivre. Que vous soyez un étudiant qui découvre la finance quantitative ou quelqu'un cherchant une remise à niveau, ce petit guide est fait pour vous.
Objectif : Nous souhaitons déterminer la juste valeur d’une option d’achat européenne sur une action sans dividende en construisant un portefeuille de couverture continu qui empêche tout arbitrage et, par conséquent, est sans risque.
Étape 1 : Nous construisons un portefeuille de couverture
Π = V(S, t) - ΔS (équation 1)
où V est la valeur de notre option d’achat, dépendant du prix de l’action sous-jacente S et du temps t.
Étape 2 : Nous considérons le changement instantané de la valeur de notre portefeuille de couverture pour évaluer le prix de l'option en fonction de la volatilité de l'action sous-jacente à tout moment (couverture continue)
dΠ = dV - ΔdS (équation 2)
Étape 3 : Nous définissons le changement instantané dans le prix de l’action sous-jacente
dS = μS dt + σS dW (équation 3)
Terme de dérive : μS dt, terme déterministe. Le terme de dérive est le taux de rendement attendu de l'action.
Terme stochastique / de diffusion : σS dW. Ce terme capture les mouvements aléatoires (stochastiques) du prix de l'action, et W est le mouvement brownien (processus de Wiener).
μ et σ représentent respectivement le taux de rendement et la volatilité.
dW capture la composante aléatoire et imprévisible des mouvements de prix.
Étape 4 : Nous utilisons le lemme d'Itô pour trouver la différentielle d'une fonction d'un processus stochastique. Le lemme d'Itô est l'analogue stochastique de la règle de la chaîne en différentiation standard
dV = (∂V/∂t) dt + (∂V/∂S) dS + (1/2) (∂²V/∂S²) (dS)² (équation 4)
∂V/∂t est appelé "thêta"
∂V/∂S est appelé "delta"
(1/2) (∂²V/∂S²) est appelé "gamma"
Étape 5 : Nous élevons au carré le terme (dS) de l’équation (3) et obtenons
(dS)² = (μS dt + σS dW)²
= μ²S² (dt)² + 2μσS² (dt dW) + σ²S² (dW)²
Note sur les règles de multiplication :
(dt)² = 0
(dt dW) = 0
(dW dW) = dt
Ainsi :
(dS)² = 0 + 0 + σ²S² dt = σ²S² dt (équation 5)
Étape 6 : Nous substituons le terme (dS)² de l’équation (4) par le terme (dS)² de l’équation (5)
dV = (∂V/∂t) dt + (∂V/∂S) dS + (1/2) σ²S² (∂²V/∂S²) dt
ou en simplifiant :
dV = (∂V/∂t) dt + (∂V/∂S) dS + (1/2) σ²S² (∂²V/∂S²) dt (équation 6)
Étape 7 : Nous substituons le terme dV de l’équation (2) par le terme dV de l’équation (6)
dΠ = dV - Δ dS
= [(∂V/∂t) dt + (∂V/∂S) dS + (1/2) σ²S² (∂²V/∂S²) dt] - Δ dS
= [(∂V/∂t) + (1/2) σ²S² (∂²V/∂S²)] dt + [(∂V/∂S) - Δ] dS
Nous posons Δ = dV/dS pour que (dV/dS - Δ)dS = 0, et nous obtenons finalement :
dΠ = (dV/dt + 1/2 * σ^2 * S^2 * d²V/dS²) dt (équation 7)
Ainsi, notre portefeuille de couverture continu ne dépend que d’un terme déterministe et est donc isolé du changement de prix de l’action sous-jacente.
Étape 8 : Puisque notre portefeuille de couverture est sans risque (équation 1), nous pouvons poser
dΠ = r Π dt avec r = taux sans risque
et nous substituons le terme Π de l’équation (1) dans l’équation (8) :
dΠ = r (V - ΔS) dt
=> dΠ = r (V - (dV/dS) S) dt (d’après l’étape 7)
=> dV/dt + 1/2 * σ^2 * S^2 * d²V/dS² = r V - r S dV/dS
=> dV/dt + r S dV/dS + 1/2 * σ^2 * S^2 * d²V/dS² - r V = 0 (Équation de Black-Scholes PDE)
L'équation aux dérivées partielles de Black-Scholes est ainsi dérivée :
dV/dt + r S dV/dS + 1/2 * σ^2 * S^2 * d²V/dS² - r V = 0

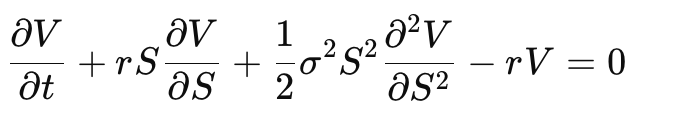
Écrire commentaire