In quantitative finance, one of the main challenges is valuing conditional derivative instruments, such as options whose price depends on specific conditions like future market prices, volatility, or other criteria.
A key aspect of evaluating these instruments correctly is the convergence of price functions. Convergence here means that the sequence of a derivative’s values "stabilizes" toward a precise value as calculations are refined. As we approach the maturity date or the conditional event, the value of the derivative should converge to a unique price.
Compact and Closed Sets in ℂ
To ensure convergence, mathematical notions of compact and closed sets are applied within the complex number space (\( \mathbb{C} \)). A compact set is both closed and bounded, ensuring that sequences of values do not diverge to infinity but remain within a defined space. This property is crucial in financial models to guarantee the convergence of derivative price functions.
Analytic Functions in Quantitative Finance
Analytic functions play a crucial role in modeling derivative prices as they provide continuous and smooth representations. A function \( f(z) \) is analytic in a domain \( D \) if it can be represented as a power series:
\[\ f(z) = \sum_{n=0}^{\infty} a_n (z - z₀)^n \]
Here, \( a_n \) are the coefficients, and \( z₀ \) is the center of the series. Analytic functions are infinitely differentiable and exhibit controlled behavior, which simplifies the valuation of derivatives. The convergence of their power series is guaranteed on compact sets within their domain of analyticity.
The Cauchy Integral Formula
The Cauchy integral formula provides a powerful method to compute the value of an analytic function at any point \( z₀ \) inside a closed contour \( \gamma \) 1. The formula states:
\[ f(z₀) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(z)}{z - z₀} \, dz \]
Here:
- \( f(z) \): Analytic function defined in the domain containing \( \gamma \).
- \( \gamma \): Closed, oriented contour in the complex plane enclosing \( z₀ \).1
- \( z₀ \): Point inside \( \gamma \) where \( f(z₀) \) is evaluated.
Example:
Let \( f(z) = \frac{1}{z} \), and consider the unit circle \( \gamma \) defined by \( |z| = 1 \) in the complex plane. Using the Cauchy integral formula to compute \( f(0.5) \), we have:
\[ f(0.5) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(z)}{z - 0.5} \, dz\]
Here, the integral evaluates the average of \( f(z) \) along \( \gamma \), illustrating how the value at \( z₀ \) depends on the function’s values on the boundary.
Implications in Finance
The Cauchy integral formula enables the evaluation of derivative prices based on their behavior along a boundary (e.g., market data over a time interval or a price range). This transforms a global pricing problem (values throughout a domain) into a local one (values only on the contour), simplifying analysis.An intuitive way to understand Cauchy’s formula is to see the integral along γ as a "weighted average" of the function’s values on the contour.
In financial terms, this means that observing prices or conditions along an interval may be sufficient to infer derivative prices within the boundary. For instance, if option prices are known at specific strikes, their values at intermediate strikes can be deduced through interpolation informed by Cauchy’s formula.
The convergence of price functions and the behavior of analytic functions are central to the valuation of conditional derivatives. Compactness ensures stability, while the Cauchy integral formula enables efficient computation by focusing on boundary values.These mathematical tools provide robust methods to infer and analyze derivative prices, supporting more accurate and stable financial models.

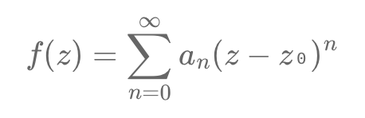
Écrire commentaire