Arithmetic vs. Continuous Compounding in Simple Terms

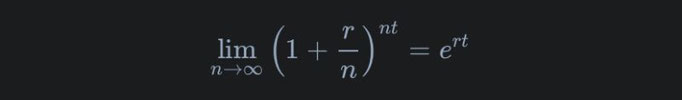
In finance, compounding describes how an investment grows over time by earning interest on both the principal and the accumulated interest. The two main methods are arithmetic (discrete) compounding and continuous compounding.

Arithmetic compounding involves applying interest at regular intervals like annually, semi-annually, quarterly, or monthly. The formula for arithmetic compounding is:

\( FV = P \times (1 + \frac{r}{n})^{n \times t} \)

Where:

FV = Future value
P = Principal
r = Annual interest rate
n = Number of compounding periods per year
t = Number of years

For example, $1,000 invested at a 5% annual rate compounded quarterly for one year:

\( FV = 1000 \times (1 + \frac{0.05}{4})^{4 \times 1} \approx 1050.95 \)

As the number of compounding periods increases, the investment grows slightly more.

Continuous compounding happens when compounding occurs an infinite number of times within a year. Mathematically, as n approaches infinity:

\( \lim_{n \to \infty} (1 + \frac{r}{n})^{n \cdot t} = e^{rt} \)

Where "e" (approximately 2.71828) represents the maximum growth. The formula for continuous compounding is:

\( FV = P \times e^{rt} \)

Using the same example, $1,000 at 5% compounded continuously for one year:

\( FV = 1000 \times e^{0.05} \approx 1051.27 \)

Comparison:

1. Annual Compounding: \( FV = 1050 \)
2. Semi-Annual: \( FV \approx 1050.63 \)
3. Quarterly: \( FV \approx 1050.95 \)
4. Monthly: \( FV \approx 1051.16 \)
5. Continuous: \( FV \approx 1051.27 \)

As compounding frequency increases, the future value grows, with continuous compounding achieving the highest possible accumulated value for a given interest rate.