Hedging strategies are crucial for managing risks related to financial instruments, especially when dealing with complex options. In this article, we explore a practical scenario involving a bank that sold a Down-and-Out European Call (DOC) option to a client. To ensure fair pricing and risk management, the bank employs the concept of put-call symmetry. We'll introduce the concept, provide a hedging formula, and present a step-by-step numerical example to illustrate the process, with a focus on the scenario where the barrier is hit before expiration.
Understanding Put-Call Symmetry:
The formula for put-call symmetry is as follows:
C(K) * K^(-1/2) = P(H) * H^(-1/2)
Where:
• C(K) represents the value of a European call option with a strike price K.
• P(H) represents the value of a European put option with a strike price H.
• K is the strike price of the call option.
• H is the strike price of the put option.
• The exponent -1/2 represents the reciprocal square root.
Put-call symmetry is based on the relationship between the payoffs of call and put options with the same strike price. This relationship holds under certain assumptions, such as no arbitrage opportunities and a specific symmetry condition between call and put option prices.
The bank can utilize the following formula to hedge and price the sold DOC option:
DOC(K,H) = C(K) - KH^(-1) * P(H^2/K) [Where H < K]
Where:
- DOC(K,H) represents the payoff of the down-and-out call option with a strike price K and a barrier H.
- C(K) is the value of a European call option with strike price K.
- P(H^2/K) is the value of a European put option with a strike price determined by H^2 divided by K.
- H is the barrier level.
Suppose a bank sold a Down-and-Out European Call (DOC) option to a client, with the following parameters:
- Strike Price (K): $100
- Barrier Level (H): $95
- Time to Maturity: 1 year
1. Calculate the Adjusted Put Strike Price:
- H^2 = $95 * $95 = $9025
- Adjusted Put Strike Price = H^2 / K = $9025 / $100 = $90.25
2. Construct the Hedging Portfolio:
- The bank acquires the call option (C(K)) for hedging purposes so that he can pay the client if the barrier of the down and out call is not hit and the call expires ITM
- The bank sells (writes) the put option (P($90.25)) for hedging purposes so that if the barrier is hit the replicating portfolio may be liquidated with a payoff of 0
3. Barrier Hit and Liquidation:
- In the scenario where the barrier is hit before expiration, making the DOC option worthless, the bank's replicating portfolio should be liquidated.
- The bank ensures that the proceeds from selling the call are exactly offset by the cost of buying back the put, as guaranteed by put-call symmetry.
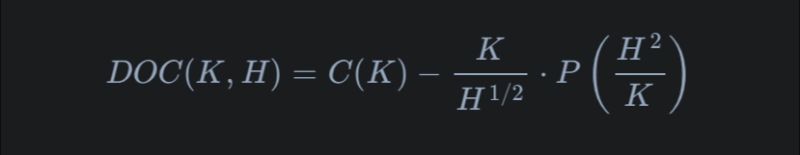

Écrire commentaire