Discrete Time
In discrete time, the random variable takes on distinct values at specific points or intervals. The expected value for a discrete random variable \( X \) is calculated as:
E[X] = \(\sum_{i} x_i P(X = x_i)\)
Where, \( x_i \) represents the possible values of \( X \), and \( P(X = x_i) \) is the probability of \( X \) taking the value \( x_i \).
In continuous time, the random variable can take on any value within a certain range. The expected value for a continuous random variable \( X \) is calculated as:
E[X] = \(\int_{-\infty}^{\infty} x f_X(x) dx\)
Here, \( f_X(x) \) is the probability density function (PDF) of \( X \).
In both cases, the general idea of the MGF is to calculate the average value of the function \( e^{tX} \) with respect to the probability distribution of \( X \), where \( t \) is a real number representing a parameter.
The Moment Generating Function is defined as:
\[ M_X(t) = \mathbb{E}[e^{tX}] \]This formula represents the expected value of the exponential of the random variable \( X \) for all possible values of \( X \) across its entire range. By calculating \( M_X(t) \), we gain a complete picture of the distribution of \( X \).
Moments of the distribution can be derived by differentiating the MGF with respect to \( t \) and evaluating at \( t = 0 \):
-
First moment (mean): \( E[X] = M_X'(0) \)
- Second central moment (variance): \( \text{Var}[X] = E[(X - E[X])^2] = M_X''(0) - (M_X'(0))^2 \)
Differentiating the MGF provides the moments of \( X \), enabling us to calculate statistical properties such as the mean, variance, and higher moments.
Example: Stock Price Changes
Imagine you're analyzing the changes in the price of a stock over a given period. These changes are modeled as a random variable \( X \), which we assume follows a normal distribution:
\[ X \sim N(\mu, \sigma^2) \]
The MGF of a normal random variable is given by:
\[ M_X(t) = e^{\mu t + \frac{1}{2} \sigma^2 t^2} \]By differentiating \( M_X(t) \), we can derive the mean and variance:
- Mean: \( E[X] = \mu \)
- Variance: \( \text{Var}[X] = \sigma^2 \)

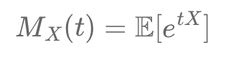
Écrire commentaire